'data.frame': 32 obs. of 11 variables:
$ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
$ cyl : num 6 6 4 6 8 6 8 4 4 6 ...
$ disp: num 160 160 108 258 360 ...
$ hp : num 110 110 93 110 175 105 245 62 95 123 ...
$ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
$ wt : num 2.62 2.88 2.32 3.21 3.44 ...
$ qsec: num 16.5 17 18.6 19.4 17 ...
$ vs : num 0 0 1 1 0 1 0 1 1 1 ...
$ am : num 1 1 1 0 0 0 0 0 0 0 ...
$ gear: num 4 4 4 3 3 3 3 4 4 4 ...
$ carb: num 4 4 1 1 2 1 4 2 2 4 ...Introdução
Continuando nossa série voltada para análise bivariada, hoje iremos estudar como avaliar a relação entre duas variáveis numéricas. Esta talvez seja a relação mais simples de se entender. A dificuldade aqui não está em compreender se as variáveis são correlacionadas ou não. A dificuldade está em identificar se existe causalidade nesta correlação.
Durante um estudo estatístico, foi encontrada uma correlação de 96% entre as Vendas Globais de Coca-Cola e o número de Divórcios no Brasil entre os anos de 2003 e 2016. À primeira vista, isso poderia levar a suposições hilárias de que o consumo de Coca-Cola está relacionado ao aumento das taxas de divórcio no país. No entanto, essa correlação é um exemplo claro de uma correlação espúria (fonte: correlacoesespurias.com.br).
Uma correlação em estatística busca medir a força com que duas variáveis estão relacionadas e também a direção desta relação (positiva ou negativa).
Vamos trabalhar com o data frame de exemplo mtcars que já vem disponível por default junto com a instalação do R:
Uma variável numérica x outra variável numérica
Vamos iniciar nossa análise tentando compreender se existe alguma relação entre as variáveis hp (horse power ou cavalos de força) e a variável mpg (miles per gallon ou milhas por galão). Ambas as variáveis são numéricas, sendo a primeira uma variável quantitativa discreta e a segunda uma variável quantitativa contínua.
A primeira vista pode parecer uma afirmação óbvia que, quanto mais potente for o motor de um carro maior será o consumo de combustível e por consequência menor será a quantidade de milhas por galão (no Brasil estaríamos falando de km por litro). Conseguimos, por intuição até mesmo dizer a direção dessa relação: quanto maior a quantidade de cavalos de força menor a quantidade de milhas por galão percorrida. Ou seja, a relação é negativa.
Podemos validar nossa intuição através de um gráfico (e geralmente no dia a dia é exatamente isso que acontece):
plot(df$hp,df$mpg)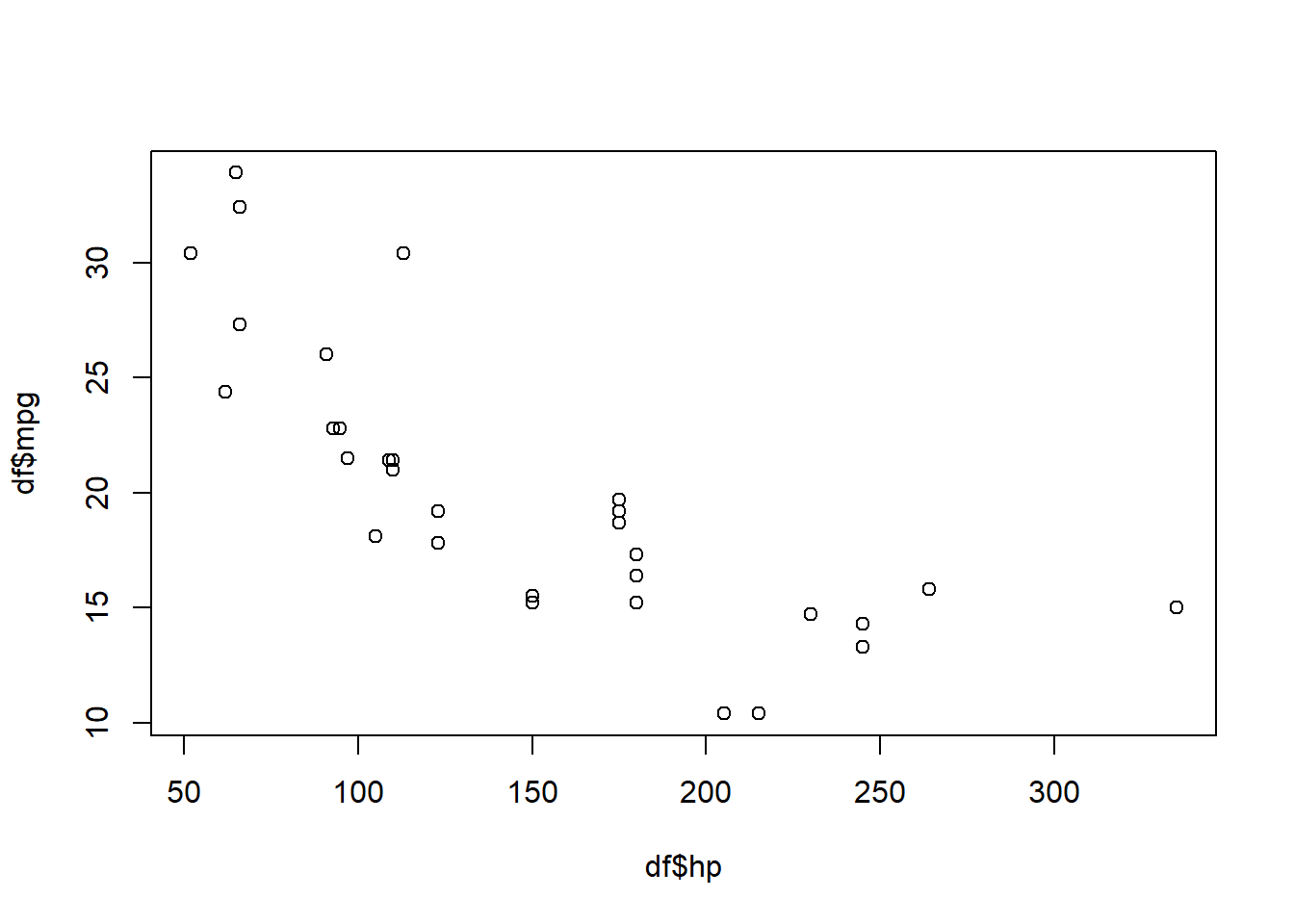
Apesar de confirmada nossa hipótese inicial, ainda não conseguimos dizer por intuição o quão forte é essa relação. E é aí que a estatística entra no jogo, para mensurar a força desta relação e nos ajudar a tomar decisões com base em dados, ao invés de nos basearmos somente em achismos.
A forma mais usual de fazer a análise de correlação de duas variáveis quantitativas é através do Coeficiente de Correlação de Pearson. O Coeficiente de Correlação de Pearson nos informa a direção da relação entre duas variáveis (positiva ou negativa) e a força desta relação através de uma medida que varia entre -1 e 1. Abaixo temos uma referência para medir a intensidade de força da relação estudada:
- 0,9 para mais ou para menos indica uma correlação muito forte
- 0,7 a 0,9 positivo ou negativo indica uma correlação forte
- 0,5 a 0,7 positivo ou negativo indica uma correlação moderada
- 0,3 a 0,5 positivo ou negativo indica uma correlação fraca
- 0 a 0.3 positivo ou negativo indica uma correlação desprezível
Finalmente podemos executar nosso comando no R e entender o quão forte é essa relação:
cor(df$hp,df$mpg, use="complete.obs")[1] -0.7761684É eu sei, parece que tivemos esse trabalhão todo para executar um comando que possui três caracteres apenas. Mas não desanime, na verdade essa é uma das vantagens de se trabalhar com R.
Nossas variáveis possuem uma relação forte negativa (-0,77) e seria importante estudar também o relacionamento das mesmas com as demais variáveis do data frame se estivéssemos pensando, por exemplo em criar um modelo.
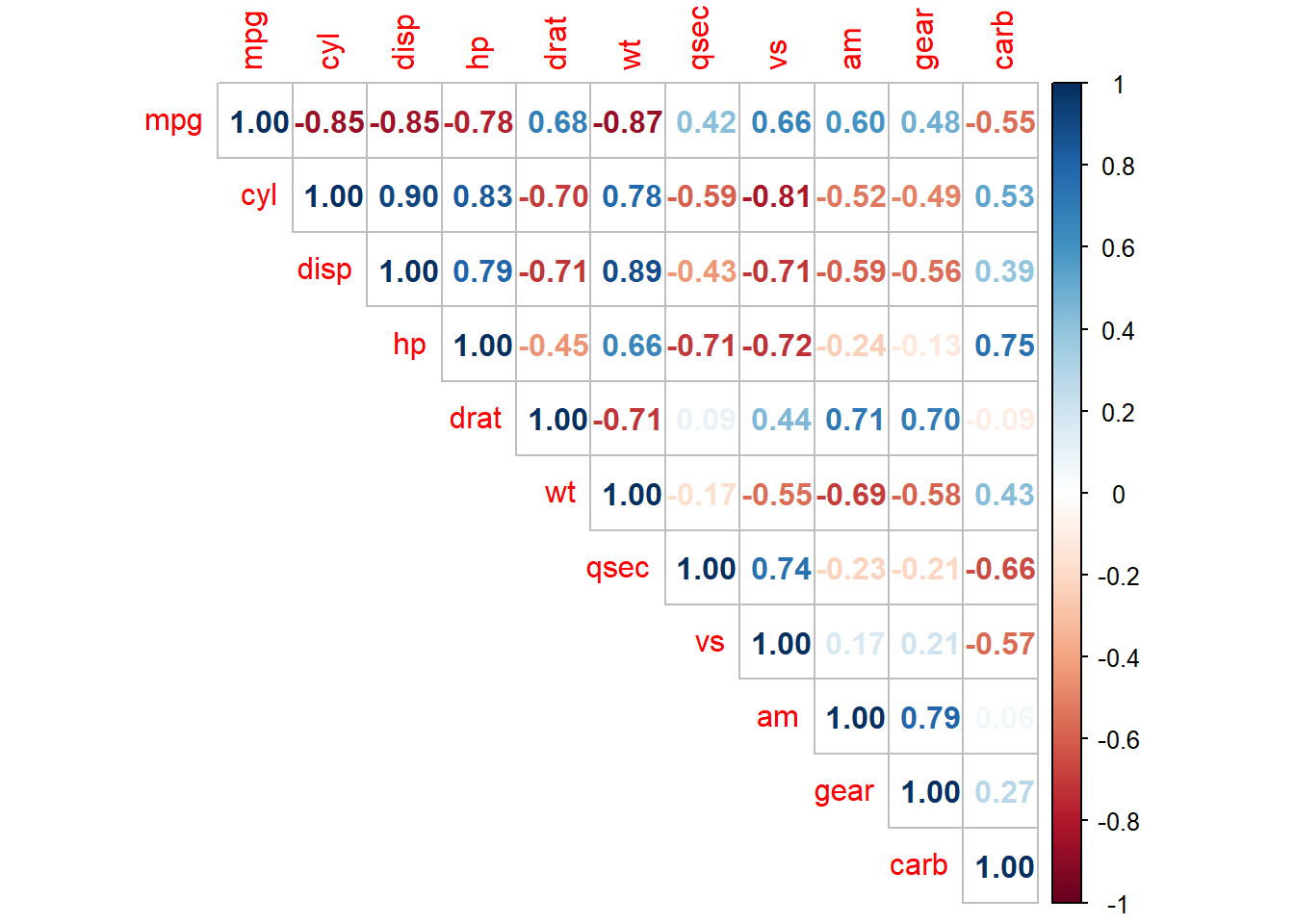
Pra finalizar, deixo vocês com o comando corrplot da biblioteca corrplot. Ela pode ser utilizada em data frames que possuam variáveis exclusivamente quantitativas (como é o nosso caso) e nos dá uma visão geral das relações dentro do data frame:
library(corrplot)
corrplot(cor(df),
method = "number",
type = "upper"
)
Por hoje paramos por aqui. Em outro artigo, finalizando nosso estudo de análise bivariada iremos estudar as relações entre uma variável categórica x outra variável numérica.
Os pacotes utilizados neste artigo foram: DescTools, corrplot além de comandos do R base.
Obrigado e boas análises!
