'data.frame': 561 obs. of 9 variables:
$ ID_IMOVEL : int 1 2 3 4 5 6 7 8 9 10 ...
$ BAIRRO_IMOVEL : chr "Santa Rosa" "Santa Rosa" "Santa Rosa" "Recanto Mar" ...
$ METRAGEM : int 140 90 130 50 70 110 90 240 210 70 ...
$ TIPO_IMOVEL : chr "Apartamento" "Apartamento" "Casa" "Apartamento" ...
$ VALOR_VENDA : int 517000 427000 558000 354000 416000 468000 436000 509000 692000 395000 ...
$ INCIDENCIA_LUZ : chr "Pouca" "Pouca" "Pouca" "Pouca" ...
$ VAGAS_GARAGEM : int 2 2 5 2 NA NA NA 1 4 2 ...
$ FLUXO_VEICULOS : chr "Intenso" "Intermediário" "Baixo" "Intenso" ...
$ COMERCIOS_RAIO_1KM: int 19 13 11 NA 26 27 18 13 24 31 ...Introdução
Entender quais variáveis existem no seu data frame e como elas se relacionam é um dos principais objetivos em se realizar uma análise exploratória dos seus dados. Dedicar um bom tempo a essa atividade, realizando uma análise cuidadosa irá aumentar o seu conhecimento sobre seu objeto de estudo, facilitar a identificação de padrões ocultos e quem sabe até permitir que você identifique novas oportunidades de negócio.
Por isso, vale muito a pena entender como essas relações podem ser mensuradas e quais testes podemos fazer para validar as descobertas realizadas. Afinal, quem faz análise de dados busca gerar respostas a problemas de negócio com embassamento teórico que direcione a tomada de decisão. Achismos de uma forma geral não tem nada a ver com o nosso dia a dia.
Baseado no tipo de dados que estamos trabalhando a análise poderá envolver:
- Uma variável categórica x outra variável categórica
- Uma variável numérica x outra variável numérica
- Uma variável categórica x outra variável numérica
Vamos utilizar um data frame fictício de imóveis. Abaixo temos uma amostra do mesmo:
Uma variável categórica x outra variável categórica
Vamos iniciar nossa análise tentando compreender se existe alguma relação entre o tipo de imóvel (Casa ou Apartamento) e a incidência de luz (nenhuma, pouca ou muita).
Ambas as variáveis são categóricas, sendo a primeira uma variável categórica nominal e a segunda uma variável categórica ordinal.
Podemos aproveitar, agora que temos esse entedimento e “ajudar” o R a lidar com essa informação, definindo qual a ordem de mensuração desta variável categórica ordinal:
dados$INCIDENCIA_LUZ <- factor(dados$INCIDENCIA_LUZ, order = TRUE,
levels = c("Nenhuma", "Pouca", "Muita"))Agora podemos criar uma tabela de contingêcia envolvendo estas duas variáveis. Esta tabela representa os valores observados para as duas variáveis em estudo e nos traz uma primeira ideia da volumetria envolvida.
tabela_contingencia <- table(dados$TIPO_IMOVEL, dados$INCIDENCIA_LUZ)
tabela_contingencia
Nenhuma Pouca Muita
Apartamento 105 106 112
Casa 50 81 107Também podemos avaliar as proporções envolvidas totalizando os dados por linha:
prop.table(tabela_contingencia, margin = 1)
Nenhuma Pouca Muita
Apartamento 0.3250774 0.3281734 0.3467492
Casa 0.2100840 0.3403361 0.4495798Ou fazer a mesma análise, só que agora totalizando os dados por coluna:
prop.table(tabela_contingencia, margin = 2)
Nenhuma Pouca Muita
Apartamento 0.6774194 0.5668449 0.5114155
Casa 0.3225806 0.4331551 0.4885845Aparentemente podemos dizer que existe uma proporção maior de apartamentos com nenhuma incidência de luz e uma proporção maior de casas com muita incidência de luz solar. A grande questão é: essa análise é realmente verdadeira? É possível afirmar, dentro de um nível de significância estatístico que essa relação de fato existe?
A resposta é sim! Através do teste qui-quadrado podemos comparar o valor observado e o valor esperado de duas variáveis categóricas. Quanto mais as frequências observadas divergirem das frequências esperadas maior será a estatística do teste do qui-quadrado e maior será a relação entre as duas variáveis.
Agora vamos entender o resultado do teste qui-quadrado:
chisq <- chisq.test(tabela_contingencia)
chisq
Pearson's Chi-squared test
data: tabela_contingencia
X-squared = 10.331, df = 2, p-value = 0.00571Devemos compreender o teste qui-quadrado como um teste de hipótese onde:
- Ho: as variáveis são independentes (não existe relação entre elas)
- Ha: as variáveis são dependentes (existe uma relação entre as mesmas)
A um nível de significância de 0,05 podemos afirmar que existe uma relação entre as variáveis estudadas. O nível de significância, ou alfa, é a probabilidade de rejeitarmos a hipótese nula (Ho) quando ela é verdadeira.
Como o valor-p resultante do teste qui-quadrado é menor que alfa (0,00571 < 0,05), rejeitamos a hipótese nula e assumimos que existe uma dependência entre as variáveis.
Os resíduos (ou resíduos de Pearson) retornam as variáveis que mais contribuem para o resultado da estatística de teste qui-quadrado:
round(chisq$residuals, 3)
Nenhuma Pouca Muita
Apartamento 1.668 -0.161 -1.255
Casa -1.943 0.187 1.462Podemos também analisar graficamente os resíduos:
corrplot(chisq$residuals, is.cor = FALSE)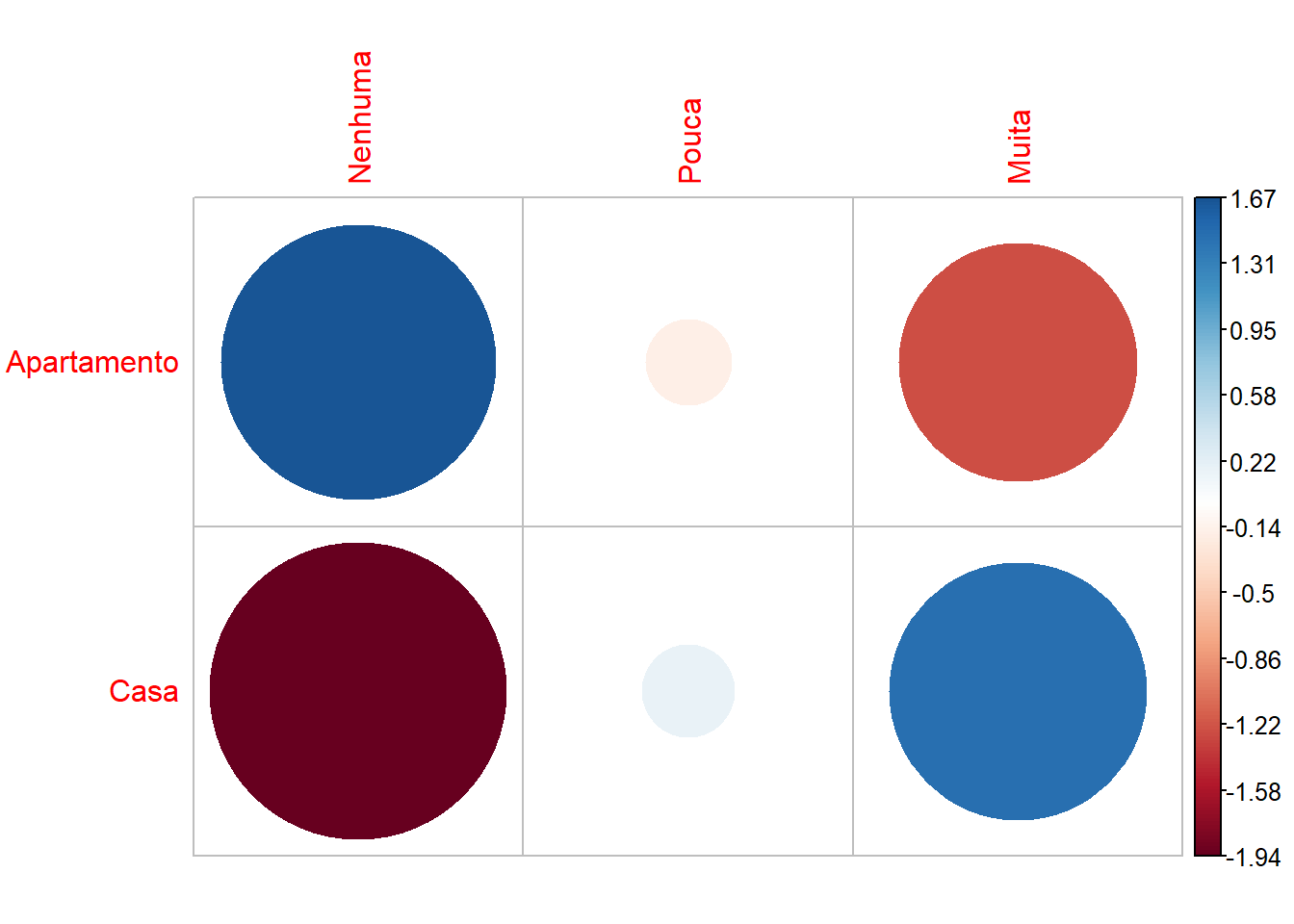
Por fim, podemos avaliar a contribuição percentual de cada variável dentro da relação estudada:
contrib <- 100*chisq$residuals^2/chisq$statistic
round(contrib, 3)
Nenhuma Pouca Muita
Apartamento 26.932 0.250 15.242
Casa 36.551 0.339 20.686Por hoje paramos por aqui. Em outros artigos iremos estudar a análise bivariada entre uma variável númerica x outra variável numérica e por fim a análise bivariada entre uma variável categórica x outra variável numérica.
Os pacotes utilizados neste artigo foram: DescTools, corrplot além de comandos do R base.
Obrigado e boas análises!
